

Finer output voltage levels could easily be produced by using a multi-positional switch and increasing the number of resistive elements within the potential divider network, therefore increasing the number of discrete switching steps. So for example, the output voltage will be 2 volts, 3 volts, 5 volts, etc.
#BINARY NUMBERS INTERACTIVE SOUNDBYTE MEDIA SERIES#
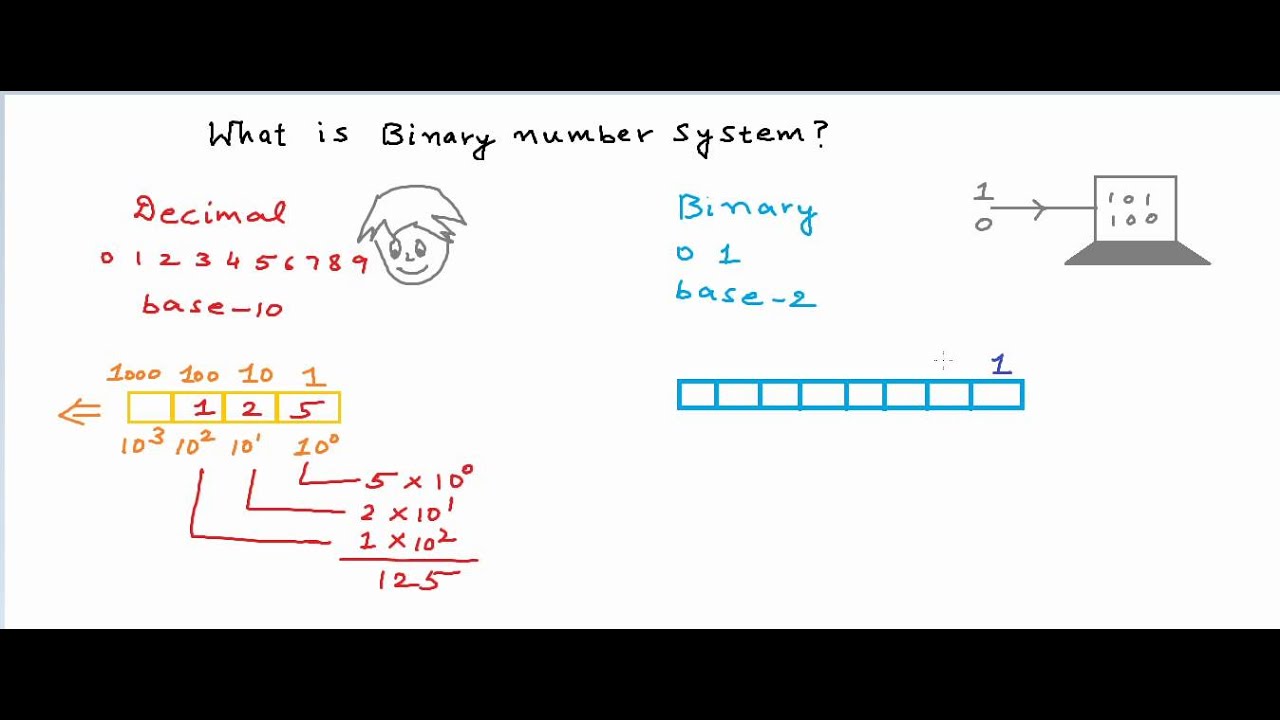
In this digital circuit example, the potentiometer wiper has been replaced by a single rotary switch which is connected in turn to each junction of the series resistor chain, forming a basic potential divider network.Īs the switch is rotated from one position (or node) to the next the output voltage, V OUT changes quickly in discrete and distinctive voltage levels representing multiples of 1.0 volts on each switching action or step, as shown in the output graph. Examples of analogue signals include temperature, pressure, liquid levels and light intensity. The output voltage can vary either slowly or rapidly from one value to the next so there is no sudden or step change between two voltage levels thereby producing a continuously variable output voltage. The output from the potentiometer varies as the wiper terminal is rotated producing an infinite number of output voltage points between 0 volts and V MAX. Electronic circuits and systems can be divided into two main categories. But what makes a signal or voltage “Digital” and how can we represent these “HIGH” and “LOW” voltage levels. A binary number system uses both of these two states.ĭigital waveforms or signals consist of discrete or distinctive voltage levels that are changing back and forth between these two “HIGH” and “LOW” states. In digital systems theses voltages are called “logic levels” and ideally one voltage level represents a “HIGH” state, while another different and lower voltage level represents a “LOW” state. The voltages used to represent a digital circuit can be of any value, but generally in digital and computer systems they are kept well below 10 volts. So instead of powers of ten, ( 10 n ) for example: 1, 10, 100, 1000 etc, binary numbers use powers of two, ( 2 n ) effectively doubling the value of each successive bit as it goes, for example: 1, 2, 4, 8, 16, 32 etc. The binary number system is a Base-2 numbering system which follows the same set of rules in mathematics as the commonly used decimal or base-10 number system. Binary Bits of Zeros and Onesīecause there are only two valid Boolean values for representing either a logic “1” or a logic “0”, makes the system of using Binary Numbers ideal for use in digital or electronic circuits and systems. These two discrete voltage levels representing the digital values of “1’s” (one’s) and “0’s” (zero’s) are commonly called: BInary digi TS, and in digital and computational circuits and applications they are normally referred to as binary BITS. Generally, a logic “1” represents a higher voltage, such as 5 volts, which is commonly referred to as a HIGH value, while a logic “0” represents a low voltage, such as 0 volts or ground, and is commonly referred to as a LOW value. Digital circuits process signals that contain just two voltage levels or states, labelled, Logic “0” and Logic “1”. Unlike a linear or analogue circuit such as AC amplifiers which process signals that are constantly changing from one value to another, for example amplitude or frequency.

Conveniently, binary numbers have only two digits that are 0 and 1, so every piece of data (number) can be represented using a binary numbering system. Data in digital circuits and computers is stored and transmitted as a series of zeros and ones and so various numbering systems are used to represent the data.


 0 kommentar(er)
0 kommentar(er)
